前言
本文将带领你了解什么是密码学,密码学都是神秘而富有冒险色彩的世界。本文素材部分来自于《classical and contemporary cryptology》。
那么,我们开始吧。
什么是密码学
假如发件人和收件人两个人分隔两地,但两人之间又需要共享一些机密信息,这就要求他们之前进行通讯。在通讯过程中,不法份子有能力截获他们之前的通讯信息。那么,发件人决定以某种她和收件人都知道的密码,来编写她和收件人的信件,然后发送给收件人,收件人在收到这封用密码写成的信件后,根据他们之间约定的密码,把这封信件翻译成可读的内容。在传递过程中,即使不法份子拿到这封信件,并知道了其中的内容,也不能明白其中要表达的是什么意思,这就达到了通讯加密的效果。
通俗一点的比喻就是,发件人把信放在一个上了锁的箱子里,然后寄给收件人。在寄送途中,不法份子拿到了这个箱子,但他没有钥匙,打不开箱子,这样就不能够知道箱子里信件的内容,他不得不把这个箱子原封不动的转交给收件人,收件人拿到箱子后,用钥匙把锁打开,轻易的就拿到了信件并知道了发件人要传递给他的什么信息了。
发件人用密码写信件(对箱子上锁)的过程,我称之前加密,收件人通过密码把信息翻译成普通人可读的内容(把箱子上的锁打开)称之为解密,加密与解密就构成了密码学。
密码学已经存在几千年的历史,后面我们将一步一步的深入了解。在我们了解密码学的时候,我们需要了解两个概念,“数论”及“概率论”。
概率论
假设骰子有6个面,分别是1、2、3、4、5、6,你猜中某一个数的概率就是1/6。
那么扔出一对(即[1,1]、[2,2]、[3,3])的概率呢?两个骰子,分别有6个面,组合起来一共就是36种组合方式,对子占了6种,所以猜中对子的概率同样是1/6,[1,1]的概率则是1/36。
那么三点([即[1,1,1]、[2,2,2])呢?三点一共只有6种组合,但所有组合却有216种,所以猜中任意相同三点的概率是1/36,某一点(豹子[6,6,6])的概率则是1/216。
用在赌博中尤其有效,你可以根据组合的奖励比例,然后和概率进行比较,就能找到奖励比概率更高的进行投注,科学的投注,想不赢都难。
恺撒密码
恺撒密码是一种最简单且最广为人知的加密技术。它是一种替换加密的技术,明文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后被替换成密文。例如,当偏移量是3的时候,所有的字母A将被替换成D,B变成E,以此类推。这个加密方法是以恺撒的名字命名的,当年恺撒曾用此方法与其将军们进行联系。
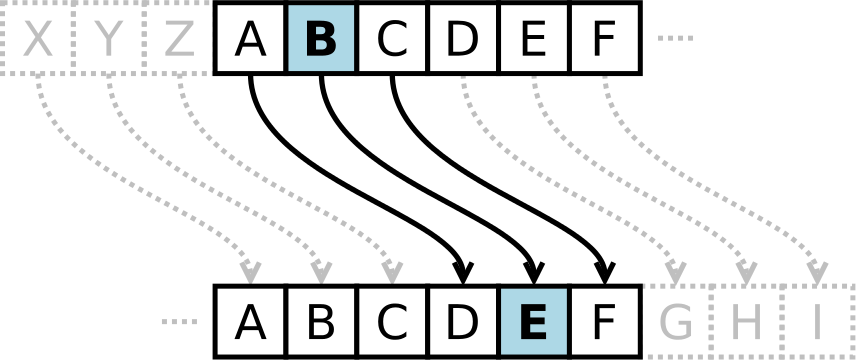
例子
恺撒密码的替换方法是通过排列明文和密文字母表,密文字母表示通过将明文字母表向左或向右移动一个固定数目的位置。例如,当偏移量是左移3的时候(解密时的密钥就是3):
明文字母表:ABCDEFGHIJKLMNOPQRSTUVWXYZ
密文字母表:DEFGHIJKLMNOPQRSTUVWXYZABC
使用时,加密者查找明文字母表中需要加密的消息中的每一个字母所在位置,并且写下密文字母表中对应的字母。需要解密的人则根据事先已知的密钥反过来操作,得到原来的明文。例如:
明文:THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
密文:WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ
破解
然而根据水桶原理,盛水的多少由最低的木片决定,密码学也有其最弱的环节。
恺撒密码在发明及使用800年后,由阿拉伯数学家Al-Kindi破解。如果你扫描任何一本英文书籍,对英文字母进行频率统计,就能发现一个非常一致的规律,那就是英文字母的使用频率是几乎固定的(中文也几乎一样),我们只需要对加密后的密文进行统计,按照频率分步进行位移推算,就能推算出偏移量,然后进行破解了。
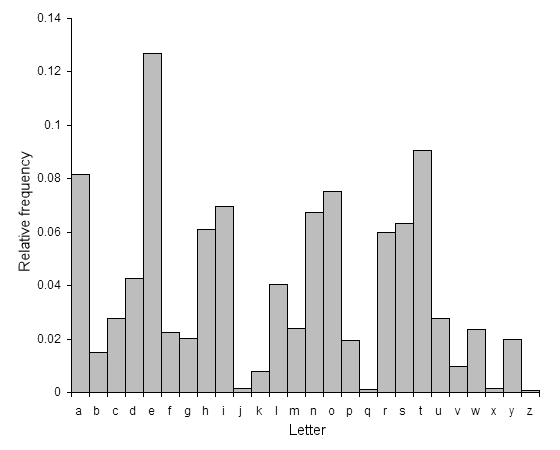
我们称这种方式为频率分析,但是频率分析也有其局限性,它对于较短或故意省略元音字母或者其他缩写方式写成的明文加密出来的密文进行解密并不适用。
另外,通过多次使用恺撒密码来加密并不能获得更大的安全性,因为使用偏移量A加密得到的结果再用偏移量B加密,等同于使用A+B的偏移量进行加密的结果。
多表密码
维吉尼亚密码是使用一系列凯撒密码组成密码字母表的加密算法,属于多表密码的一种简单形式。
在一个恺撒密码中,字母表中的每一字母都会作一定的偏移,例如偏移量为3时,A就转换为了D、B转换为了E……。而维吉尼亚密码则是由一些偏移量不同的恺撒密码组成。
为了生成密码,需要使用表格法。这一表格包括了26行字母表,每一行都由前一行向左偏移一位得到。具体使用哪一行字母表进行编译是基于密钥进行的,在过程中会不断地变换。

例子
例如,假设明文为:
ATTACKATDAWN
选择某一关键词并重复而得到密钥,如关键词为LEMON时,密钥为:
LEMONLEMONLE
对于明文的第一个字母A,对应密钥的第一个字母L,于是使用表格中L行字母表进行加密,得到密文第一个字母L。类似地,明文第二个字母为T,在表格中使用对应的E行进行加密,得到密文第二个字母X。以此类推,可以得到:
明文:ATTACKATDAWN
密钥:LEMONLEMONLE
密文:LXFOPVEFRNHR
破解
对包括维吉尼亚密码在内的所有多表密码的破译都是以字母频率为基础的,但直接的频率分析却并不适用。例如,如果P是密文中出现次数最多的字母,则P很有可能对应E(前提是明文的语言为英语)。原因在于E是英语中使用频率最高的字母。然而,由于在维吉尼亚密码中,E可以被加密成不同的密文,因而简单的频率分析在这里并没有用。
破译维吉尼亚密码的关键在于它的密钥是循环重复的。如果我们知道了密钥的长度,那密文就可以被看作是交织在一起的恺撒密码,而其中每一个都可以单独破解。使用卡西斯基试验和弗里德曼试验来得到密钥的长度。
假设密钥为secret,其长度为6,我们需要对全部信息进行统计,检查不同间隔的频率分布,当我们检查到间隔为6的频率分布时,就能匹配上文字的分布频率,现在的问题就是要破解6个恺撒密码的偏移量而已,然后根据这6个恺撒密码破译密文,整个工作需要的只是时间而已,在现在计算机的计算能力面前,只不过是秒秒种的事情。
这也只是频率分析的变种。
其实我们早期的密保卡就是一个多表加密的典型例子。
一次一密
我们要怎样避免由频率分布而造成密码被破译呢?答案就是随机。
我们知道英文总共有26个字母,所以当使用恺撒密码的时候,偏移量最多也只有26种情况,而使用维吉尼亚密码,也只不过是把这种情况变得更多而已。
但,当我们对加密的文字每个字母都取随机的偏移量时,即10字的密文就给一组10个长度的随机数,情况就不同了。解密者可以根据这组随机数轻易的破译这组密文。但拦截都如果想破译这10个字符,则有141167095653376种情况,因为每个字符的偏移量都是随机的,所以根本不能用频率分析进行破解,而暴力破解的工作量太大,等你破解出来的时候,也许这个信息已经过时了。

